Total numbers of question is 77 Multiple Choice Questions
Results
#1. Which triangles are classify based on the sides?
Select all that apply:
#2. Which triangles are classify based on the angles?
#3. A ____ of a triangle is a line segment that joins a vertex to the mid-point of the side that is opposite to that vertex.
#4. An ____ of a triangle is a line segment that starts from the vertex and meets the opposite side at right angles.
#5. How many medians can a triangle have?
#6. Does a median lie wholly in the interior of the triangle?
#7. How many altitudes can a triangle have?
#8. Will an altitude always lie in the interior of a triangle?
#9. Can you think of a triangle in which two altitudes of the triangle are two of its sides?
#10. Can the altitude and median be same for a triangle?
Ex. equilateral triangle
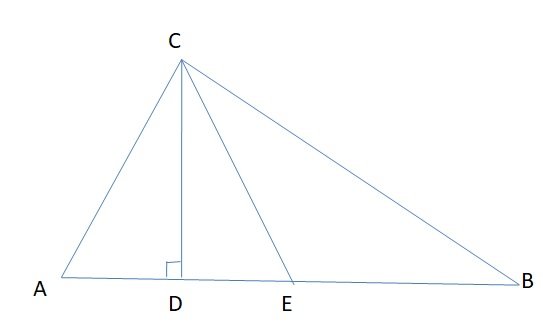
In ∆ ABC, E is the mid-point of AB. Write the name of line segments
#11. CD is _________.
#12. CE is _____
#13. Is AD = DB
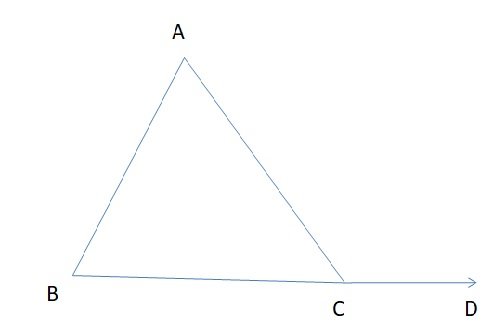
#14. ∠ACD is called an ___ angle of the ∆ABC formed at vertex C.

#15. ∠ACB is called an ___ angle of the ∠ACD

#16. ∠A and ∠B are called the two _____ opposite angles of ∠ACD.

#17. ∠ACD = sum of ____
#18. Can the exterior angle of a triangle be a straight angle?
#19. The total measure of the three angles of a triangle is ____°.
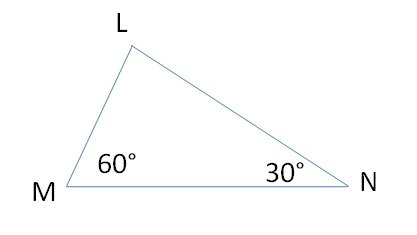
#20. Find the value of x in given triangle.
#21. Two angles of a triangle are 20º and 80º. Its third angle will be ____º .
#22. One of the angles of a triangle is 70º, if other two angles are equal. then value of other angles will be ___0º.
The three angles of a triangle are in the ratio 1:2:1. Find all the angles of the triangle.
#23. 1st angle ____°.
#24. 2nd angle ____°.
#25. 3rd angle ____°.
#26. Can you have a triangle with two right angles?
#27. Can you have a triangle with two obtuse angles?
#28. Can you have a triangle with two acute angles?
#29. an you have a triangle with all the three angles greater than 60º?
#30. Can you have a triangle with all the three angles less than 60º?
#31. A triangle in which all the three sides are of equal lengths is called an ____ triangle.
#32. A triangle in which two sides are of equal lengths is called an ____triangle.
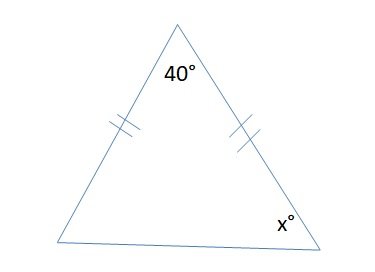
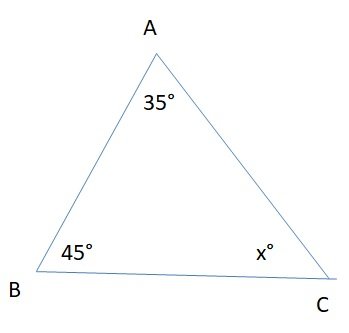
#33. Find the angle x in given figure.
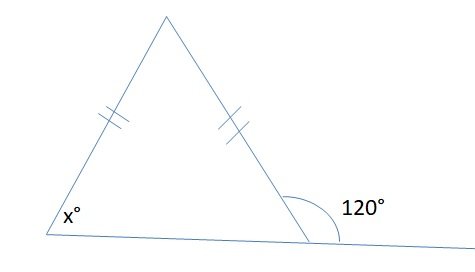
#34. Find the angle x in given figure.
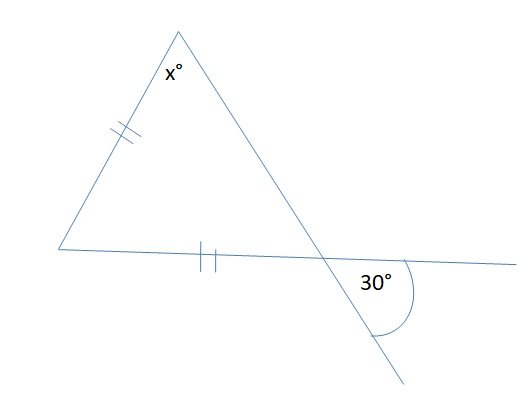
#35. Find the angle x in given figure.
#36. The sum of the lengths of any two sides of a triangle is ___ than the third side.
#37. Is there a triangle whose sides have lengths 10.2 cm, 5.8 cm and 4.5 cm?
#38. The lengths of two sides of a triangle are 6 cm and 8 cm. Between which two numbers can length of the third side fall?
Is it possible to have a triangle with the following sides?
#39. 2 cm, 3 cm, 5 cm
#40. 3 cm, 6 cm, 7 cm
#41. 6 cm, 3 cm, 2 cm
Take any point X in the interior of a triangle ABC. Is
#42. AX + BX > AB?
#43. BX + XC > BC?
#44. AX + XC > AC?
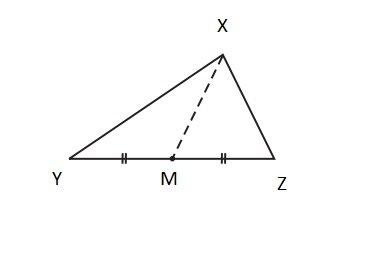
#45. XM is a median of a triangle XYZ. Is XY + YZ + ZX > 2 XM?
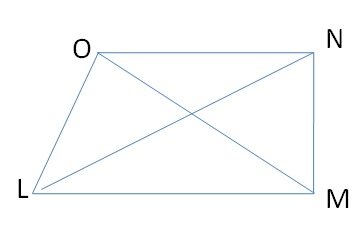
#46. LMNO is a quadrilateral. Is LM + MN + NO + OL > LN + MO?

#47. LMNO is quadrilateral. Is LM + MN + NO + OL < 2 (OM + LN)?
In a right-angled triangle, the sides have some special names.
#48. The side opposite to the right angle is called the _____.
#49. The other two sides are known as the ___ of the right-angled triangle.
#50. Pythagoras property only holds when the triangle is _____
#51. Determine whether the triangle whose lengths of sides are 4 cm, 4 cm, 5 cm is a right-angled triangle.
#52. XYZ is a triangle, right-angled at X. If XY = 3 cm and XZ = 4 cm, then YZ=___cm.
#53. A 5 m long ladder reached a window 4 m high from the ground on placing it against a wall at a distance a. The distance of the foot of the ladder from the wall will be ___m..
#54. Is 2 cm, 2 cm and 5 cm can be the sides of a right triangle?
#55. A tree is broken at a height of 3 m from the ground and its top touches the ground at a distance of 4 m from the base of the tree. Find the original height of the tree. ____m
#56. Find the perimeter of the rectangle whose length is 4 m and a diagonal is 5 m. (____m)
#57. The diagonals of a rhombus measure 8 m and 6 m. Its perimeter will be ____ m.